Enhancing security in digital design

Towards scalable and practical solutions

Mingfei Yu and Giovanni De Micheli

Data plays a crucial role in driving innovation and efficiency across various domains. However, the concern of losing control over private information leads to data contributors’ hesitance to cooperate. The importance of data evidences the necessity of investigating secure computation techniques, such as garbled circuits (GC) and fully homomorphic encryption (FHE), as they empower data-driven collaboration without compromising privacy. But there is no free lunch – privacy protection is generally achieved at the expense of prohibitive computational and/or communication overhead, resulting in significant losses in system performance and scalability. This project aims to facilitate practical secure computation techniques, preparing them for large-scale, low-latency, and energy-efficient application scenarios. We specifically emphasize the following aspects:

  1. Establishing the logic representation for each cryptographic protocol to accurately identify the performance bottleneck in the associated secure computation paradigm.
  2. Devising logic synthesis and optimization algorithms to manipulate the logic model, thereby enhancing the performance of the represented computation paradigm.

Less Communication is Better Than More: Low-cost Garbled Circuits Generation

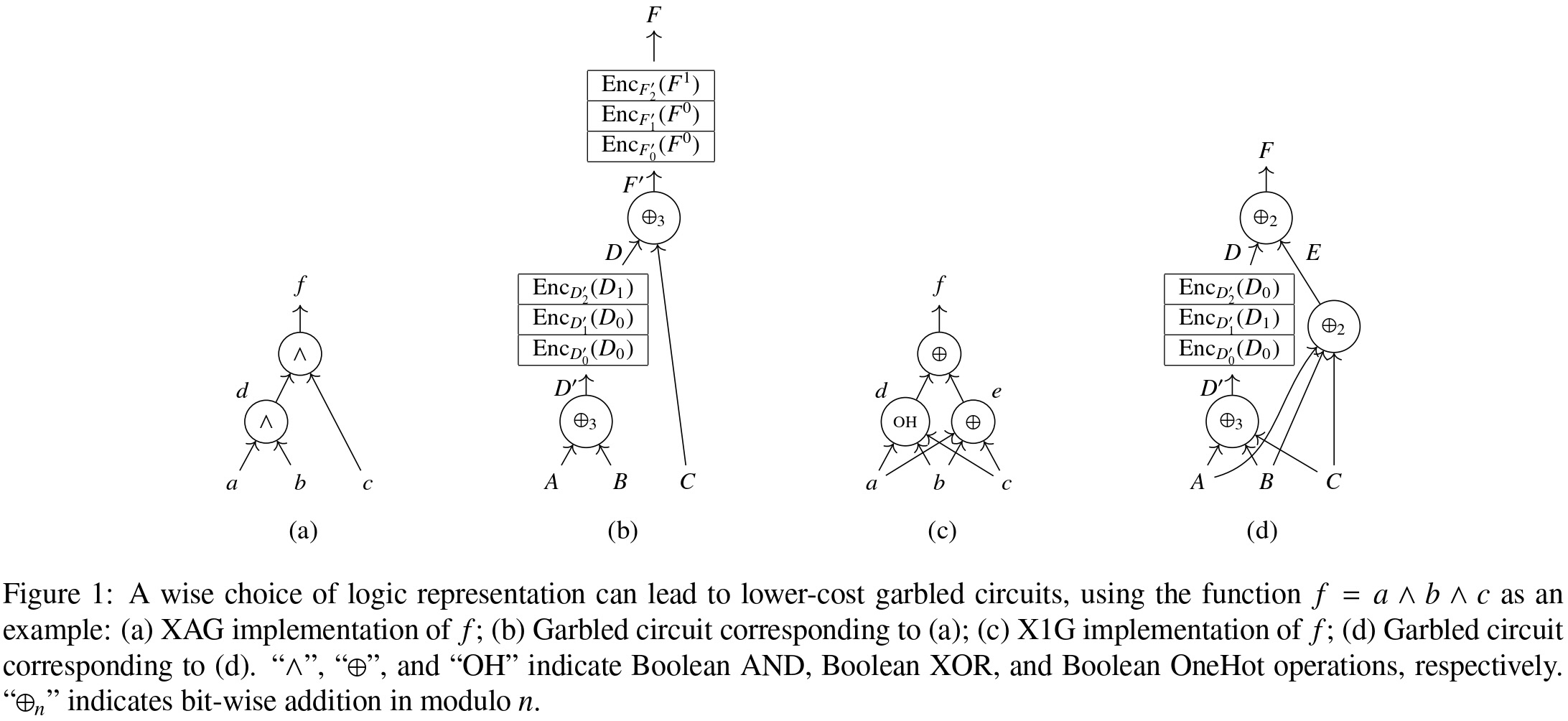
First proposed in 1986 by the Turing Award winner Andrew Yao, the garbled circuits (GC) protocol is the cornerstone of various advanced solutions to realize secure computation. Starting from representing the target computation as a Boolean circuit, the protocol protects the privacy of participants by transferring Boolean operations on truth values to look-up operations on ciphertexts, a.k.a. garbling the logic gates in the circuit. The GC protocol typically suffers from a substantial communicational overhead, due to the necessity of distributing among participants the tables holding the ciphertexts, for execution.

Our research aims to solve this bottleneck by synthesizing the Boolean circuit that implements the target computation in a ciphertext-efficient manner. Towards this goal, we have proposed:
  1. Ciphertext-efficient logic representation. Based on a thorough analysis of the expressive power of logic primitives, together with the cost to garble them, we proposed the XOR-OneHot Graph (X1G) as a ciphertext-efficient logic representation for representing Boolean functions. An example is shown in Figure 1.

    DAC_GC

    In the example, for the same computation, transitioning from XOR-AND Graph (XAG) to X1G in the logic representation reduces the communication cost in the resulting garbled circuits by half, from 6 ciphertexts to 3.
  2. Exact approach to synthesizing the optimum implementations. We formulate the problem of optimally synthesizing the X1Gs that realize the given Boolean functions, into a satisfiability (SAT) problem. The novel encoding facilitates agile implementations of small-scale functions.
  3. Efficient heuristic algorithm to optimize implementations. For large-scale computations, we develop a logic rewriting-based technique that strikes a good balance between quality and scalability.

Faster Homomorphic Operations and Beyond: Expediting Homomorphic Computation via Circuit Optimization

Fully homomorphic encryption (FHE) represents a revolutionary encryption paradigm that enables computation on ciphertexts without the need for decryption – widely regarded as the holy grail of modern cryptography.

Most modern HE schemes are based on the learning with error (LWE) problem, a hard lattice problem, and utilize noisy ciphertexts to ensure data privacy. However, as computation progresses, noise accumulates. Once noise exceeds a certain threshold, correct decryption becomes impossible. Such HE schemes are termed leveled, due to the constraint on the allowed number of homomorphic operations to be involved. Leveled HE schemes are parameterized. A parameter selection would allow a larger noise budget at the cost that each involved homomorphic operation is rather computationally intensive. While the concept of FHE dates back to 1978, the first realization did not come until the ground-breaking bootstrapping theorem by Craig Gentry in 2009. In his blueprint, bootstrapping refreshes the noise level within a ciphertext by homomorphically executing the decryption function, elevating leveled HE into the realm of FHE. Yet, bootstrapping’s computational demand remains high.

With the computation paradigm modeled as a circuit of additions and multiplications, a.k.a. a homomorphic circuit, an effective strategy to enhance the practicality of leveled HE schemes entails reducing the levels of the circuit. In particular, homomorphic multiplication introduces significant noise, making minimizing the multiplicative depth (MD) pivotal. Lower MD offers flexible security parameters, hence accelerating each homomorphic operation. Meanwhile, lower MD commonly comes at the cost of higher multiplicative complexity (MC), leading to more homomorphic multiplications and potentially slowing down the overall homomorphic computation.

We introduce an MC-aware MD minimization technique, a first in the field. Evaluation on practical benchmarks showcases an average 21.32% computation time reduction, with up to 60.87% improvement – an advancement with far-reaching implications.

Main recent publications

  1. M. Yu, D. Marakkellage and G. De Micheli, Logic Synthesis Unleashes Efficient Secure Computation, MPDI Cryptography 2023, 7, 61.
  2. M. Yu and G. De Micheli, Generating Lower-Cost Garbled Circuits: Logic Synthesis Can Help, HOST, 2023.
  3. M. Yu and G. De Micheli, Striving for both quality and Speed: Logic Synthesis for practical garbled circuits, Proceedings ICCAD, 2023.
  4. E. Testa, M. Soeken, H. Riener, L. Amaru, G. De Micheli, A Logic Synthesis Toolbox for Reducing the Multiplicative Complexity in Logic Networks, DATE 2020 Grenoble, France, March 2020.

Access all publications from here.