Quantum compilation

Giulia Meuli, Fereshte Mozafari, Bruno Schmitt, Heinz Riener, Mathias Soeken, Giovanni De Micheli

Quantum computers promise to exceed the capabilities of conventional computers in fields such as computational chemistry, machine learning, and cryptoanalysis, thus attracting massive research interest. Currently, we distinguish between two different quantum computing applications. The first one is related to the quantum systems that are available at the present and in the near future. Such systems are characterized by a few noisy qubits and are called Noisy Intermediate-Scale Quantum (NISQ) systems. The second application, called fault-tolerant quantum computing, will allow us to run complex algorithms, such as Shor's algorithm for factorization, relying on error-correcting codes. Many of these algorithms require some classical arithmetic operations, e.g., exponential, reciprocal, square root, multiplication, squaring. The corresponding Boolean functions have to be mapped into a universal set of quantum gates, to be performed on an actual quantum computer. This mapping is part of the so-called quantum compilation process. The output of the process is a quantum circuit, which can be evaluated in terms of the resources it requires (gates and qubits). 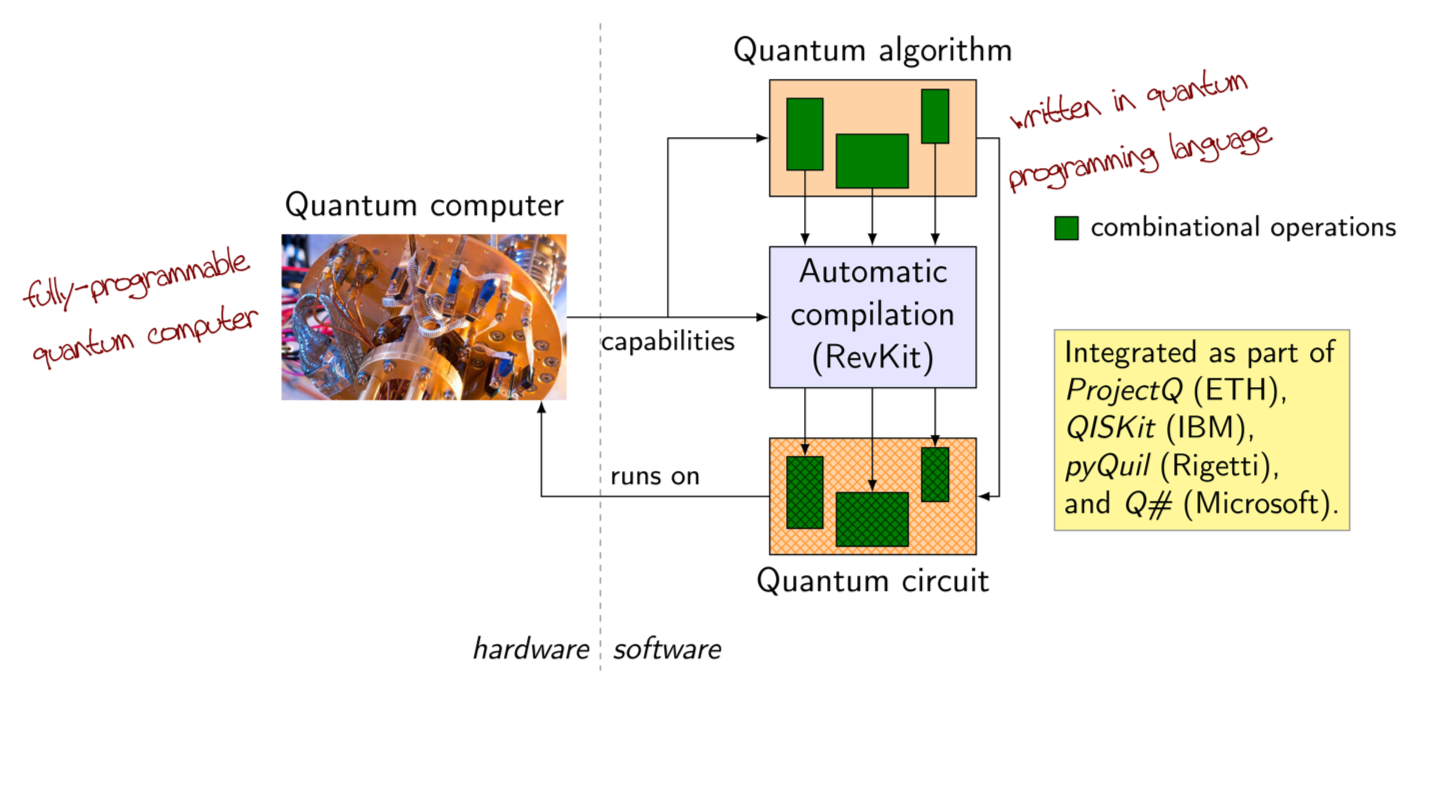QCFLOW

General design flow for quantum computing

Quantum algorithms are described in terms of quantum programs written in a quantum programming language (such as ProjectQ, Q#, Qiskit, or PyQuil). In order to run the program on a physical quantum device, the program must be translated into a sequence of elementary operations that can be run on the quantum computer. Such a sequence of quantum operations is referred to as quantum circuit. In order to cope with the complexity of a high-level quantum program, typically several levels of abstractions are required in the quantum compilation process. The choice of layers, and the choice of transformation algorithms in each layer, highly depends on whether compilation targets NISQ or fault-tolerant quantum computers. For example, NISQ quantum computers are very noisy and the decoherence time of qubits is short; therefore, it is key to find a quantum circuit that reduces 2-qubit gates, since these are more noisy than single-qubit gates. In error-corrected fault-tolerant quantum computers, the goal is to reduce the use of gates that require a large overhead in terms of error correction (e.g., the single-qubit non-Clifford T gate). Typical layers of abstractions are:

Synthesis: The task of mapping combinational logic into high-level quantum operations. In this step the aim is to meet the qubit requirements of the targeted quantum device.
Optimization: The task of optimizing a quantum circuit. A typical cost metric is to reduce the number of gates. Depending on the targeted quantum device, different gates may have a different cost. If the circuit is technology-dependent, optimization must guarantee not to violate constraints posed by the targeted device.
Mapping: The task of translating a technology-independent quantum circuit into a technology-dependent quantum circuit. The resulting circuit can only use those quantum operations which are supported by the target device and must adhere to possible coupling constraints of qubit pairs.

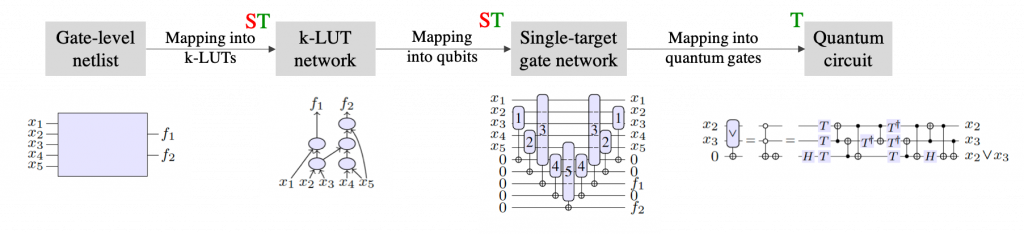
Example of quantum compilation flow for fault-tolerant quantum computing

Synthesis of quantum computing structures

The ultimate goal of quantum compilation is to bridge the gap between abstract quantum algorithms and their concrete implementation. The research focuses on using the quantum circuit model of computation. Therefore we study all the steps necessary to transform a high-level quantum algorithm, often mathematically described, into a sequence of elementary operations that can be executed by a quantum computer.

The embodiment of our research is the creation of design tools and libraries. Built using C++17, Tweedledum , and its companion Tweedledee, are two header-only, open-source libraries in development. Tweedledee offers parsers for formats commonly used to describe quantum circuits, e.g., OpenQASM and Quil. Tweedledum provides methods for composing quantum programs at the circuit level, for optimizing them in both the number of gates and the number of qubits, for transforming them for the constraints of a particular device, etc. The ongoing research on the development of Tweedledum loosely falls under one of the following four categories.

Core.
Study of different data structures and abstractions used to represent quantum circuits and gates. Internally, the library can represent circuits using netlists, DAGs, and phase polynomials. The rationale for investigating different data structures is the observation that the efficacy of some optimization routines is tightly related to the underlying data structures. Indeed, phase polynomials make the optimization of Z-axis rotation gates trivial. Furthermore, it can help optimization algorithms to escape structural bias. The use of directed acyclic graphs, on the other hand, greatly helps with rule-based optimizations and pattern matching.
Synthesis/Compilation.
In Tweedledum, there are many techniques to generate a quantum circuit, which are lousily classified as synthesis or compilation, depending on the starting point. Indeed, the difference between these two is subtle.
We call compilation the process that transforms a higher-level representation of the circuit in a lower-level representation. For example, if we start with a classical reversible logic circuit and transform it into a quantum circuit defined over a Clifford+T gate set. Another example, starting from an OpenQASM abstract-syntax tree and generating a quantum circuit. A final example would be to decompose a circuit over a Clifford+T gate set into a circuit over the CX+U3 gate set, which is required to run a circuit in an IBM's quantum computer.
In synthesis, the starting point is some other specification. We can synthesize a quantum circuit from a Boolean function. This Boolean function can be represented as a logic network, a truth table, a sum-of-products expression, etc. There are functions to synthesize circuits out of permutation matrices, or a list of parity terms, or from diagonal unitary matrices.
The choice of which compilation method or synthesis method to use is highly dependent on the cost function used to evaluate the result. A fault-tolerant cost function, for example, aims to decrease the number of T gates, as they require a large overhead in terms of error correction. A NISQ cost function is more concerned with reducing the number of two-qubit gates.
Optimization.
A significant part of research on quantum computing is working out how to run quantum circuits on real quantum machines. In these machines, experimental errors and decoherence introduce errors during computation. Thus, to obtain a robust implementation, it is essential to apply aggressive space (number of qubits) and time (number of gates) optimization techniques. The library already provides some basic optimization techniques.
Research is ongoing for new techniques based on sets of orthogonal transformations. Transformations range from purely structural, which rely only on the relationship between nodes (structure) of a netlist or directed acyclic graph representation, to purely functional, i.e., when they rely on the unitary matrix. There exists a significant tradeoff between the quality of results and scalability.
Mapping.
In the quantum circuit model of computation, circuits manipulate qubits. These qubits exist as abstractions within a circuit and shall be called virtual (or logical). Mapping is the task of finding a one-to-one relation between virtual qubits and physical qubits, which denote the actual hardware units that store quantum bits, enabling the execution of all gates. In the circuit model, any pair of virtual qubits can interact, i.e., we can perform a two-qubit operation between any pair. The physical qubits in most quantum hardware, however, are not fully connected, meaning that not every pair of physical qubits can participate in the same quantum operation. These physical connectivity restrictions are known as coupling constraints. The library divides mapping into two subtasks: placement and routing. Placement tries to find a bijection between the set of virtual qubits and the set of physical qubits, such that the quantum device can execute all gates. Such perfect placement, however, may not exist. In this case, a placement algorithm might return an initial placement. When the placement is not enough, it is necessary to transform the circuit. Given an initial placement, a router uses SWAP operations to move the virtual qubits around the device topology whenever it finds an operation that acts on qubits that are physically separated. It routes the involved virtual qubits to adjacent physical qubits.
The quality of the mapped circuit is measured in the number of swap operations. A good mapper should not add more swaps than necessary. We know the different combinations of placement strategies and routing strategies greatly influence quality. Current research aims to better understand the relation among these factors: i) metric to evaluate the quality of initial placements; ii) new initial placement heuristics, iii) new routing algorithm.

Resource estimation of quantum algorithms

This research focuses on estimating the resources required to perform quantum algorithms on a fault-tolerant quantum computer. To this purpose, we develop optimization and synthesis algorithms that are technology-agnostic, hence apply to any quantum computing system.

Compilation of combinational logic.
We focus on providing automatic tools to compile complex logic designs, required by various quantum algorithms, e.g., Grover’s, into quantum operations. The cost of the resulting quantum network can account for a large portion of the overall cost of the quantum algorithm. Hence, optimizing the synthesis outcome can have a strong impact on the overall algorithm complexity. Implementations for all the developed synthesis methods can be found in caterpillar, an open-source C++ library for quantum compilation, which is part of the EPFL synthesis libraries. Caterpillar enables a two-step approach to quantum compilation. The first step consists of building a reversible network for the given combinational design, specified as a multi-level logic network. The library supports many different types of logic networks, e.g., Xor-And-inverted Graphs (XAG), And-Inverter Graphs (AIG), Look-Up Table (LUT) networks. Many different strategies can be selected to perform this step, all exploring a different balance between qubits and gates. The second step consists of transforming each reversible gate in a quantum circuit, using manually-optimized decompositions from the literature.
Quantum memory management.
Quantum memory management is becoming a pressing problem, especially given the recent research effort to compile new and complex quantum algorithms. The only existing automatic method for quantum states clean-up relies on the availability of many extra resources. We show how this problem exactly matches the reversible pebbling game problem. Based on that, we develop a SAT-based algorithm that returns a valid clean-up strategy, taking the limitations of the quantum hardware into account. The developed techniques, embedded in Caterpillar, empower the designer with the flexibility to explore the trade-off between memory resources and number of operations.
The STG (Single-Target Gate) Benchmark.
The benchmark suite contains quantum circuits implementing small Boolean functions and expressed in the Q# quantum programming language. The circuits are optimized according to the requirements of fault-tolerant quantum computing. For each representative of a spectral-equivalent class of Boolean functions with 4 and 5 inputs, the benchmark contains three different implementations: optimized for T-count, T-depth or number of qubits. The benchmark can be used to test new optimization algorithms or in combination with hierarchical methods.

Quantum state preparation

In general, the initial quantum state is the classical basis state in which all bits are 0. Some quantum algorithms require a specific quantum state in a superposition of basis states at the beginning of the desired application-specific computation. Hence, in addition to the quantum circuit that performs the quantum algorithm, a specific quantum circuit is required that prepares the desired initial quantum state. Moreover, some quantum computing applications (e.g., quantum machine learning, and quantum chemistry) require to efficiently load large sets of classical data into quantum states. As a result, an efficient quantum state preparation is an important task in the quantum compilation.

The preparation of quantum states is performed by a quantum circuit consisting of Controlled-NOT (CNOT) and single-qubit gates. Known algorithms to prepare arbitrary n-qubit quantum states create quantum circuits in O(2ⁿ) runtime and use O(2ⁿ) CNOTs, which are more expensive than single-qubit gates in NISQ architectures or use ancilla qubits. To reduce runtime and the number of CNOTs without using ancilla qubits, we simplify the problem by considering important families of quantum states such as Uniform Quantum States (UQS) and Cyclic Quantum States (CQS).

UQSs are superpositions of basis states, where all amplitudes are either zero or have the same value. We map UQSs to Boolean functions and propose a UQS Preparation (UQSP) method. For generating such a state given as input a Boolean function f, we assume all states are zero in the beginning, and then we search for an efficient construction that transforms a given unitary matrix UQSP(f) into a circuit.

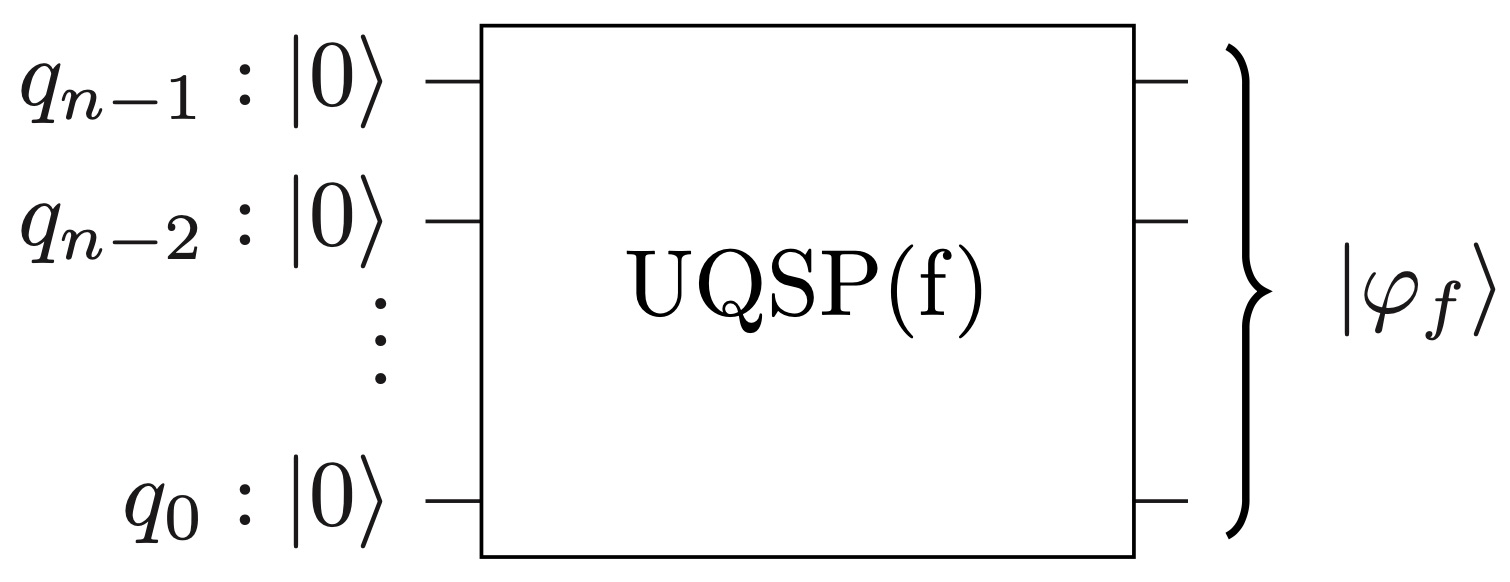
Preparing UQSs using Boolean functions allows us to utilize different representations of Boolean functions. We utilize decision diagrams to reduce runtime and enable preparation for a larger number of qubits where the state-of-the-art methods are not applicable. To further reduce the number of CNOTs, we utilize variable reordering and functional dependencies among the variables. Our state preparation method requires an exponential number of CNOTs in the worst case but it reduces CNOTs significantly for practical benchmarks. Moreover, our method generates an exact representation of quantum states without using ancilla qubits.

In particular, multipartite quantum states that are invariant under permutations, e.g. Dicke states, have intriguing properties. In another work, we consider states invariant under cyclic permutations, which we call cyclic states. We present a quantum algorithm that deterministically prepares cyclic states, with gate complexity O(n), without requiring any ancillary qubit. The idea is based on creating cyclic permutations step-by-step. We design our algorithm such that creating each permutation requires only a constant number of 2-qubit and 3-qubit gates regardless of the total number of qubits n.

This research provides an open-source C++-17 library for quantum state preparation, called angel, which is part of the EPFL synthesis libraries.

Main Publications