Versatile mapping
Logic synthesis is the task of transforming (and optimizing) a description of a digital circuit from a high-level abstraction to the interconnection of logic gates to be placed and routed. Logic synthesis entails solving computationally-intractable problems through a plurality of heuristic techniques. Logic synthesis is a necessary step in the design of integrated circuits and is highly responsible for their quality in terms of Performance, Power, and Area (P/P/A).
In the last two decades, electronic circuits and digital systems have evolved rapidly, facing many new architectural and technological changes. Consequently, Electronic Design Automation (EDA) and logic synthesis have adapted and changed to be able to accurately design the new generation of digital systems. Nowadays, logic synthesis is an important area of research for two main reasons: (i) Many and diverse ways of computation, alternative to the established CMOS technology, have been presented in the last years. Post-silicon technologies, called emerging technologies, have been shown to be feasible and may provide us with better – more efficient – electronic devices. In a similar way, novel areas of applications of logic synthesis are emerging, ranging from deep learning to cryptography and security applications. (ii) The current computing and storage means make it possible to solve exactly problems that were only approximated before. Moreover, new reasoning engines, covering from deep learning to new SAT-solvers, can be used as a mean of computation, thus possibly unlocking novel optimization opportunities and enabling hardware of higher quality.
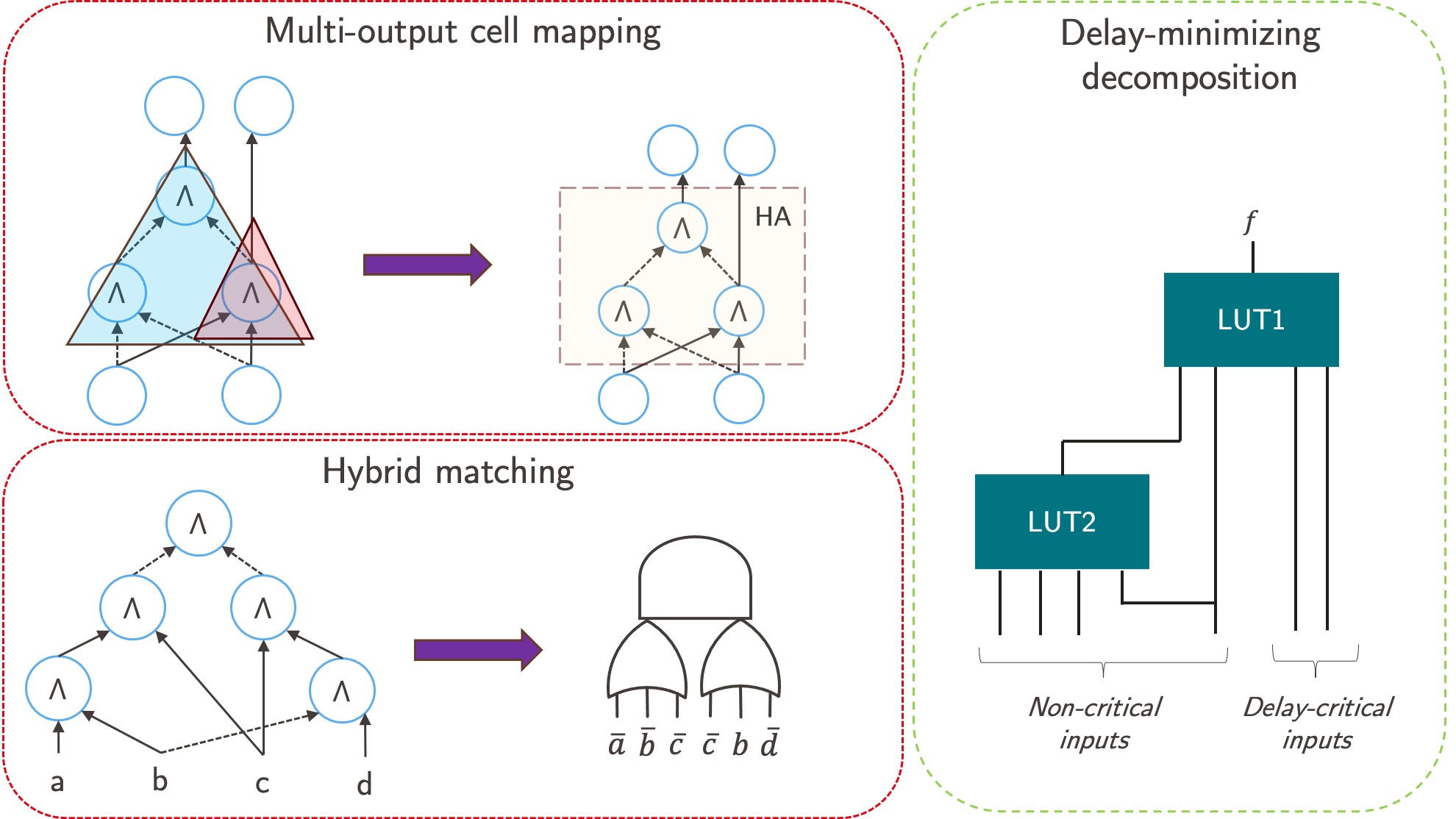
Technology mapping is a crucial step in the realization of integrated circuits. Its primary goal is to translate a technology-independent representation of digital hardware into a connection of technology-specific components, such as standard cells or lookup tables (LUTs). Researchers at LSI investigated new techniques to improve technology mapping for Application-Specific Integrated Circuits (ASICs) and Field-Programmable Gate Arrays (FPGAs).
Contributions to technology mapping for ASICs include a matching method, called hybrid matching, that associates sections of the subject graph with a list of cells that are functionally equivalent and capable of implementing those sections. Hybrid matching combines the benefits of pattern and Boolean matching, supporting large cells, such as ANDORs with over 6 inputs, and maintaining the matching precision of Boolean matching. ASICs circuits obtained using hybrid matching showed a 6% area reduction compared to Boolean matching. Furthermore, another enhancement to technology mapping integrates the support for multi-output cells, such as half adders and full adders, to improve power performance area (PPA). Regarding logic synthesis for FPGAs, we have developed a LUT mapper enhanced with a delay-driven Boolean decomposition to overcome structural bias and minimize delay. Experimental results have shown a substantial an average delay improvement of 12%, compared to conventional LUT mapping.

We search for new strategies for optimizing circuits after mapping, focusing on metrics such as area, delay, and power. Traditionally, logic synthesis optimizes circuits in two steps: first, a technology-independent circuit representation is optimized, next, the circuit is mapped to an interconnection of gates in a given technology. The motivation behind the two-step approach is the desire for higher quality and scalability. In this paradigm, the optimization of the technology-independent representation is guided by simple cost functions, that are assumed to correlate with some optimization metrics after mapping. For instance, reducing the number of gates and logic levels in the technology-independent representation is considered an effective heuristic for reducing area and delay after mapping. However, experimental evidence shows that high-effort optimization of the technology-independent representation, using the technology-independent cost functions, does not always correlate with corresponding benefits in the mapped circuit. Our research aims at i) investigating the validity of the technology-independent assumptions, ii) to introduce more technological information at the logic synthesis level, and iii) to perform logic optimization directly on mapped circuits.
This research proposes a new logic synthesis and verification paradigm based on circuit simulation. In this paradigm, high-quality, expressive simulation patterns are pre-generated to be reused in multiple runs of optimization and verification algorithms, resulting in reduced time-consuming Boolean computations such as SAT-solving. Methods to generate expressive simulation patterns are presented and compared, and a bit-packing technique to compress them is integrated into the implementation. We show that the generated patterns are reusable across different algorithms and after network incrementa improvements.
A logic synthesis algorithm, Boolean resubstitution, and a verification algorithm, combinational equivalence checking, are two examples of using this paradigm. In simulation-guided Boolean resubstitution, simulation patterns are used for efficient filtering of optimization choices, leading to a lower cost in expanding the search space. By adopting the proposed paradigm, we achieve a 5.9% reduction in the number of network graph nodes (AIG), compared to 3.7% by a state-of-the-art resubstitution algorithm, within comparable runtime. In simulation-guided equivalence checking, the number of SAT solver calls is reduced by 9.5% with the use of the expressive simulation patterns accumulated in earlier logic synthesis stages.
This research addresses the design of a versatile logic mapping and restructuring tool with two objectives: i) it can transform a logic network from one technology-independent graph representation to another; ii) it can map a logic network to a cell library.
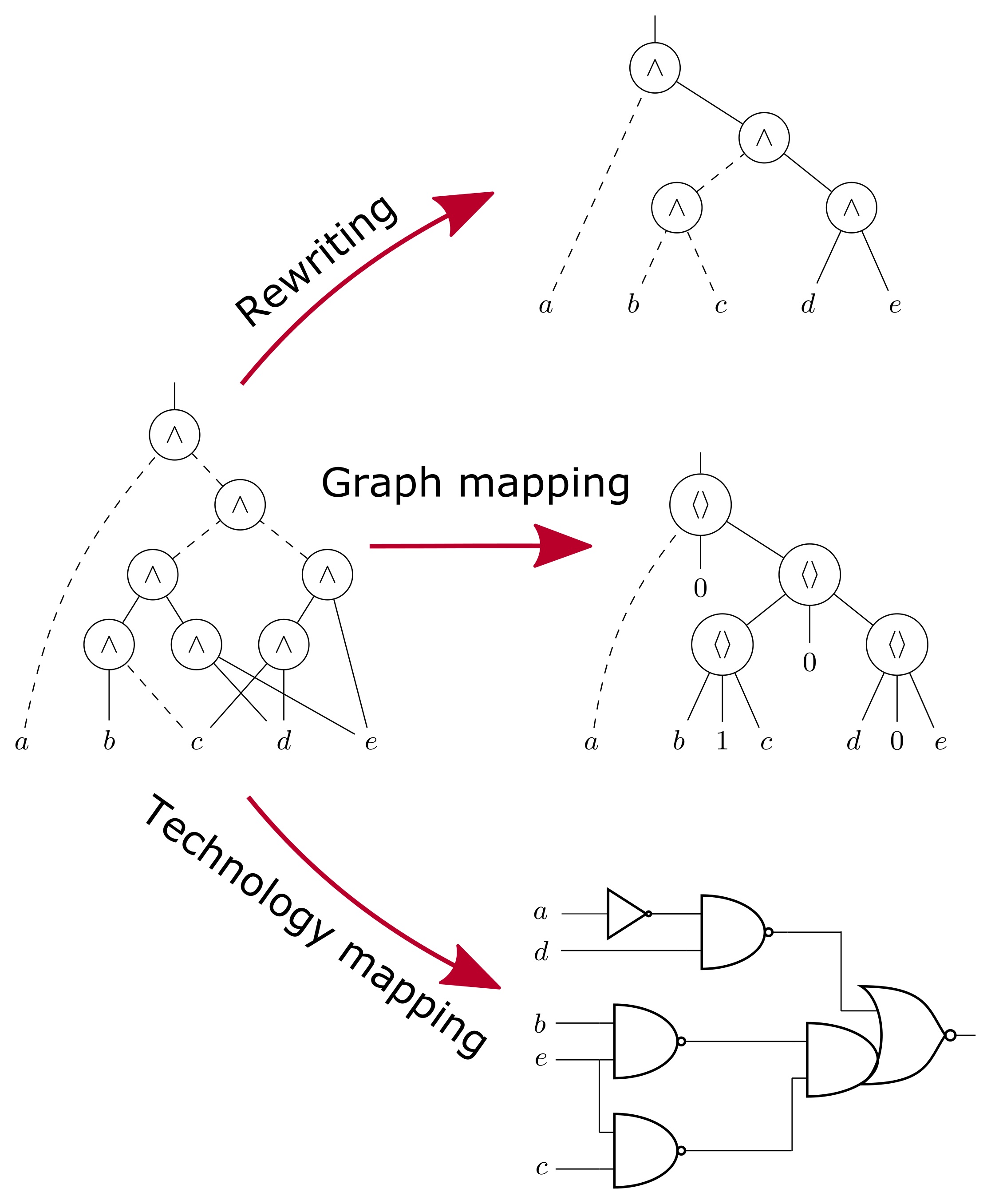
The motivation for the first task is the following. Originally, 2-input NANDs and NORs, together with inverters, were used as primitives in graph representations thanks to their universality. As logic synthesis evolved, the And-Inverter graph (AIG) became the most common technology-independent representation. As an alternative, Majority-Inverter graphs(MIGs) have been proposed and motivated by a more expressive potential and by majority-based emerging technologies, e.g., quantum-dot cellular automata. Additionally, Xor-And graphs (XAGs) and Xor-Majority graphs (XMGs) have been proposed for their compactness in arithmetic circuits and as a basis for logic rewriting. Recently, 3-input gates have also been explored as new graph representations to address logic synthesis.
Since multiple graph representations are available to support logic synthesis, we developed the first mapper that supports mapping across graph representations and cell libraries while optimizing the circuit for delay or area. Thus, these steps support the mapping of networks of various kinds to cell libraries. Our mapper can also be used as an optimization tool for logic restructuring.
In the experiments, we showed that our approach enables an average reduction up to 27% and 40 % in size and depth respectively when mapping for size reduction from AIGs to MIGs in the EPFL benchmark suite. We then showed that our approach leads to better results when used for logic restructuring reducing the average size by 10% and 14% further as compared to LUT-based rewriting and cut rewriting methods. Finally, we map to a standard cell library and compare it to ABC showing an average improvement of 1.75%, 0.10%, and 18% in area, delay, and total run-time respectively.
Pushing the idea of using 3-input primitives even further, we have studied the suitability of other 3-input gates as logic primitives. There are ten 3-input NPN classes that depend on all three variables. In this regard, we have evaluated the expressive powers of different 3-input logic functions and shown that the 3-input Dot ( x xor (z or xy)) and Onehot ( xy’z’ xor x’yz’ xor x’y’z) gates exhibit the highest expressibility.

The high expressive power of Dot gates yields concise logic representations, and hence, Dot-Inverter Graphs (DIG) are attractive candidates for technology-independent intermediary logic representations. Optimization algorithms can run faster with less memory on smaller logic representations. Moreover, this also inspires emerging technologies to consider physical implementations of Dot gates.
Our current research focuses on developing improved synthesis algorithms for these non-traditional representations. Specifically, we try to understand the manipulation capabilities of homogenous logic representations with different 3-input primitives.
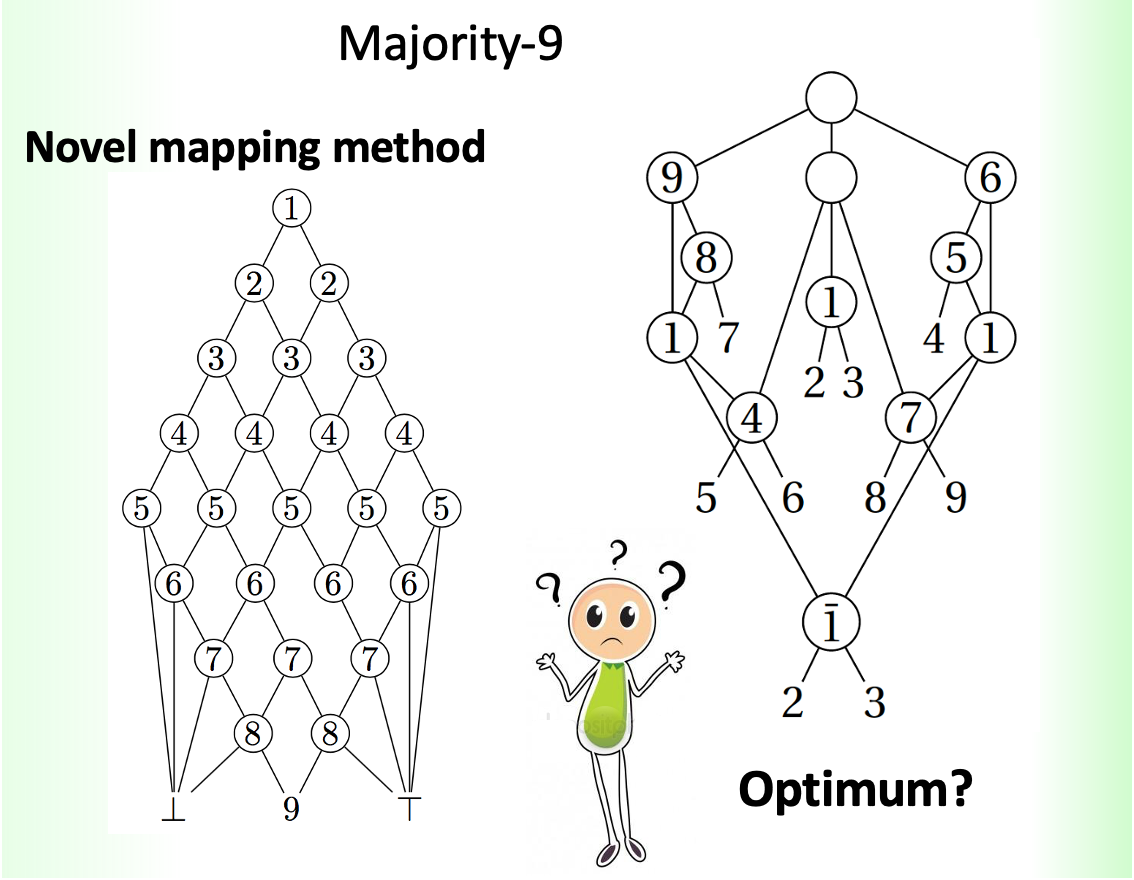
The majority function is a logic function of an odd number of inputs that evaluates to TRUE if the number of inputs assigned to TRUE outnumbers those assigned to FALSE. For typical 3-input functions, the function is TRUE when at least two of its inputs evaluate to TRUE, and thus used to compute the carry in adders. The majority function has frequently been studied as a central primitive in logic synthesis applications for many decades. As an example, Donald Knuth refers to the majority function as “probably the most important ternary operation in the entire universe.” Despite many years of study, effective EDA tools based on the majority function were developed only recently at EPFL/LSI. Current research at LSI investigates majority-based logic synthesis from both a theoretical and a practical perspective. We develop new algorithms to optimize logic networks based on majority logic, and find new ways on decomposing large majority operations into networks of smaller ones.
The new data structures and optimization methods researched at EPFL/LSI are mainly based on majority and comparator logic connectives. We have demonstrated large improvements in contemporary CMOS design, especially for arithmetic circuits. Indeed, majority and comparators are the basis for arithmetic. We also research algorithms for the exact decomposition of large majority functions into smaller primitives. In particular, even the decomposition of the 9-input majority function into 3-input primitives turns out to be an open problem.
Exact synthesis aims at finding optimum representations of logic circuits in some metric. As the problem is computationally intractable, only circuits of limited size can be exactly optimized. Nevertheless, exact solutions shed some light on some logic network structures.
Boolean satisfiability (SAT) solvers have made some remarkable progress in the last decade. They can now be integrated into various large-scale logic synthesis algorithms in a robust manner. At EPFL/LSI we use SAT solvers to solve the exact synthesis problem, which should find a circuit that realizes a function under some input constraints, e.g., the input gate library, the size of the network, or the depth of the network. Besides that, we also use SAT solvers to implement Boolean decomposition and classification algorithms.
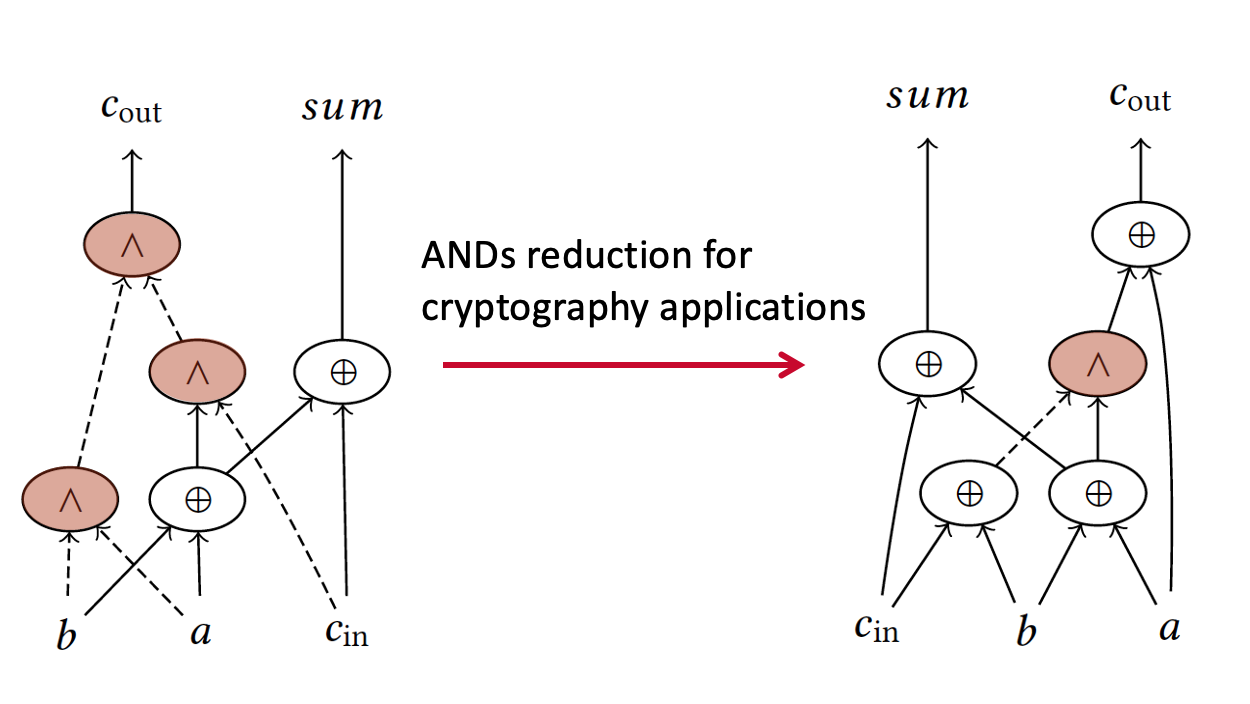
We have also established a way to measure resilience to security attacks to logic circuits. We leveraged a classic result by Boyer and Peralta linking the circuit vulnerability to the multiplicative complexity of a logic function. We devised a new automatic synthesis flow that aims at minimization of the number of AND gates in an EXOR - AND network graph (XAG) which is an upper bound on the multiplicative complexity. Our tool and methods obtain significant results over both EPFL and cryptography and security benchmarks.
EPFL/LSI has a large effort aimed at developing logic synthesis design tools, libraries and benchmarks that are made publicly available. In the last four years, we developed a collection of modular software libraries and benchmarks to support various logic synthesis applications. Nowadays, the EPFL Logic Synthesis Libraries consist of several C++ libraries designed for the development of logic synthesis applications. This includes a command-shell library (alice), a library for parsing file formats used in logic synthesis and formal verification (lorina), a library to represent logic networks (mockturtle), libraries for efficient manipulation of truth tables (kitty) and exclusive-or sum-of-products expressions (easy), an exact synthesis libraries (percy) and libraries for supporting quantum compilation (tweedledum) and quantum circuit synthesis (caterpillar). Together with these libraries, open EDA benchmarks suites have been developed to challenge existing EDA design tools in different applications.
The EPFL Logic Synthesis Libraries and Benchmarks aim at building up an active open-source community in the field of logic synthesis as well as developing a methodology to share best practices and support new libraries and benchmarks in the EDA field. The libraries provide state-of-the-art solutions for standard tasks that can be readily composed in a plug-and-play fashion to address advanced synthesis and verification problems. This allows scientists to focus on more complex tasks in their research and eases the comparison to the state of the art in a unified framework. The benchmarks serve as a comparative standard to evaluate the performance and quality of logic synthesis and optimization algorithms.
EPFL/LSI open source libraries are available in the logic synthesis library showcase repository.
Large-scale combinatorial logic benchmarks are available in the logic synthesis benchmarks repository and on Zenodo.
CirKit and RevKit tools for classical logic optimization and quantum compilation, respectively, are available in the CirKit and RevKit repository.
Engineering changing order (ECO) benchmarks are available here.